变分自编码 | Ugly Gardon

变分自编码（Variational Autoencoder）可以用于生成高精度的图像，我们可以从神经网络、概率图模型这两个角度去描述它。

The Neural Net Perspective

从神经网络的角度来看，VAE 包含了编码器、解码器和损失。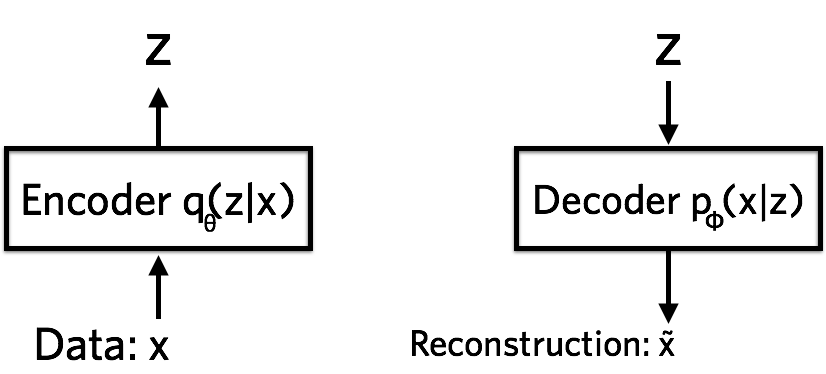

自编码器是输入 X 进行编码后得到 Z，再利用 Z 解码得到 X’。对比 X 与 X’ 的误差，利用神经网络训练使得误差逐渐减小，达到非监督学习的目的。

Encoder

编码是从高维信息降维得到低维信息的过程。可以认为是非线性的 PCA。

这里用 $q_{\theta}(z | x)$ 表示编码网络。一般可以假设它服从高斯分布。 $\theta$ 是编码网络的参数。

Decoder

解码是编码的逆向过程。

以 MNIST 数据集为例，解码器将 Z 的值解码成 784 个伯努利分布的参数，每个伯努利分布描述了一个像素点的灰度值。

用 $p_{\phi}(x | z)$ 表示解码网络。 $\phi$ 是解码网络的参数。

log-likelihood $\log p_{\phi}(x | z)$ 可以表示用 z 出重建 x 的有效程度。

Loss

整体损失为单点损失之和，

$Loss=\sum_{i=1}^{N} l_{i}$

其中单点损失可以表示为

$l_{i}(\theta, \phi)=-\mathbb{E}_{z \sim q_{\theta}\left(z | x_{i}\right)}\left[\log p_{\phi}\left(x_{i} | z\right)\right]+\mathbb{K} \mathbb{L}\left(q_{\theta}\left(z | x_{i}\right) \| p(z)\right)$

即解码器的 log-likelihood 再加一个正则项，约束编码器和先验的差距。

一般假设先验服从正态分布，并且让编码器和先验接近，这样可以让编码器尽量的分散，而不是在特定点上过拟合。

通过在损失上梯度下降，可以更新出编码网络的参数。

The Probability Model Perspective

从概率图模型的角度看，它将和变分推理的思路一致。

从观测到隐层，称为推理网络（Inference Network），即编码器；从隐层到观测，称为生成网络（Generative Network），即解码器。

KL 不易计算，因此 VI 优化 证据下界（ELBO） 来求解。

ELBO

由于观测之间不共享同一个潜变量，因此可以写出单点的 ELBO

$\mathscr{L}_{i}(\lambda)=\mathbb{E}_{q_{\lambda}\left(z | x_{i}\right)}\left[\log p\left(x_{i} | z\right)\right]-\mathbb{K} \mathbb{L}\left(q_{\lambda}\left(z | x_{i}\right) \| p(z)\right)$

可见 ELBO 与神经网络的损失表达式取反是一致的。 $\lambda$ 是变分参数。

变分参数可以选择多观测共享或不共享。

Mean-field variational inference
- no shared parameters
Amortized inference
- global parameters are shared across all datapoints

Inference Network

用推理网络进行编码，即学习出一个分布族里最接近真实后验的变分分布。

$q_{\lambda}^{*}(z | x)=\arg \min _{\lambda} \mathbb{K} \mathbb{L}\left(q_{\lambda}(z | x) \| p(z | x)\right)$

Generative Network

用生成式网络进行解码时，往往会假设

$\begin{array}{l}{p({z})=\operatorname{Normal}(0,1)} \\ {p({x} | {z})=\operatorname{Normal}\left(\mu_{\beta}({z}), \sigma_{\beta}^{2}({z})\right)}\end{array}$

where $\mu$ and $\sigma^{2}$ are deep networks with parameters $\beta$

Amortized Inference

为了让多个数据可以分批训练，假设模型有公共的变分分布，即进行摊余推理。

变分分布依赖于第 i 个数据和共享的变分参数。于是原本的 ELBO 为多个模型参数

$\mathscr{L}\left(\lambda, \phi_{1 \ldots n}\right)=\mathbb{E}_{q}[\log p(\beta, \mathbf{z}, \mathbf{x})]-\mathbb{E}_{q}\left[\log q(\beta ; \lambda)+\sum_{i=1}^{n} q\left(z_{i} ; \phi_{i}\right)\right]$

改写为

$\mathscr{L}(\lambda, \theta)=\mathbb{E}_{q}[\log p(\beta, \mathbf{z}, \mathbf{x})]-\mathbb{E}_{q}\left[\log q(\beta ; \lambda)+\sum_{i=1}^{n} q\left(z_{i} | x_{i} ; \phi_{i}=f_{\theta}\left(x_{i}\right)\right)\right]$

因此 ELBO 的目标式为

$\mathscr{L}(\nu)=\sum_{i=1}^{n} \mathbb{E}_{q\left(z_{i} ; x_{i}, \nu\right)}\left[\log p\left(z_{i}\right)+\log p\left(x_{i} | z_{i}, \theta\right)-\log q\left(z_{i} ; x_{i}, \nu\right)\right]$

Reparameterization

$\begin{aligned} \varepsilon & \sim \mathcal{N}(0,1) \\ t\left(\varepsilon, x_{i}, \nu\right) &=\varepsilon+g\left(x_{i} ; \nu\right) \end{aligned}$

$\nabla_{\nu} \mathscr{L}=\sum_{i=1}^{n} \mathbb{E}_{s(\varepsilon)}\left[\nabla_{z_{i}}\left(\log p\left(z_{i}\right)+\log p\left(x_{i} | z_{i}, \theta\right)-\log q\left(z_{i} ; x_{i}, \nu\right)\right) \nabla_{\nu} t\left(\varepsilon, \nu, x_{i}\right)\right]$

步骤

符合 BBVI 准则。

samples $\varepsilon_{i}$ for each data point and calculates $z_{i}$
uses these samples to calculate noisy gradients with respect to $\nu$ and $\theta$
follows those gradients in a stochastic optimization