变分推理与黑盒推理

Background

数据量大，如何挖掘其中的含义，找到其中的因果关系？

我们用机器学习和统计方法找到其中的联系。

流程一般是提出假设，挖掘出特征，得到预测，修改模型，提出假设……迭代进行。

概率机器学习的目标是学习出后验，即 $p(z|x)={p(z,x) \over p(x)}$。其中联合概率可以用生成式得到，关于分母则需要边缘化隐变量，因此不易求得。

Variational Inference

指数族分布
$p(x)=h(x) \exp \left\{\eta^{\top} t(x)-a(\eta)\right\}$

$\eta$ the natural parameter

$t(x)$ the sufficient statistics

$a(\eta)$ the log normalizer

$h(x)$ the base density

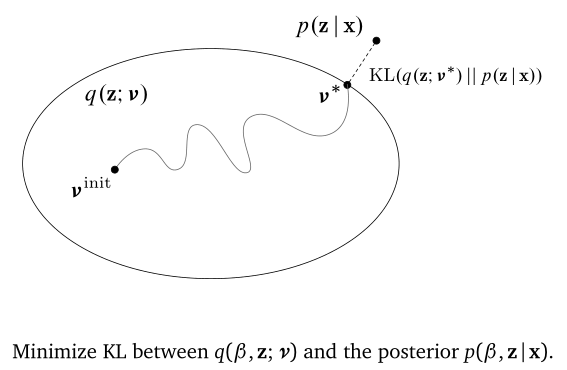
找到一个后验的近似分布 $q(z;\nu)$ 使得它们的 KL 散度尽量小。

先选择一个分布族，如指数分布族，再在该分布族里优化参数 $\nu$，使得 KL 散度最小，此时是最优的后验分布 $q(z;\nu^*)$，即

$q_{\nu}^{*}(z | x)=\arg \min _{\nu} \mathbb{K} \mathbb{L}\left(q_{\nu}(z | x) \| p(z | x)\right)$

但由于真实后验为

$p(z | x)=\frac{p(x, z)}{p(x)}$

无从计算，因此很难从优化 KL 散度的角度入手。

由于

$\log p(x)=\mathscr{L}(\nu)+\mathbb{K} \mathbb{L}\left(q_{\nu}(z | x) \| p(z | x)\right)$

可以最大化 证据下界（ELBO） 进行优化。

ELBO

$\mathscr{L}(\nu)=\underbrace{\mathbb{E}_{q}[\log p(\beta, \mathbf{z}, \mathbf{x})]}_{\text {Expected complete log likelihood }}-\underbrace{\mathbb{E}_{q}[\log q(\beta, \mathbf{z} ; \boldsymbol{\nu})]}_{\text {Negative entropy }}$

第一项相当于联合似然，要尽可能大。第二项则相当于变分分布的熵取反，使 q 分布 diffuse.

还有一种分解 ELBO 的方式：

$\mathscr{L}(\nu)=\underbrace{\mathbb{E}_{q}[\log p(\mathbf{x} | \beta, \mathbf{z})]}_{\text {Expected log likelihood of data }}-\underbrace{\operatorname{KL}(q(\beta, \mathbf{z} ; \boldsymbol{\nu}) \| p(\beta, \mathbf{z}))}_{\text {KL between variational and prior }}$

第一项相当于似然，第二项是变分分布和真实分布的 KL 散度。

注意： ELBO 不一定是凸的。

Mean-filed VI

平均场近似是指隐变量之间相互独立，则可以假设各自的分布。在优化其中一个变量时，固定住其他变量，进行优化。再迭代优化出所有变量。与 Gibbs Sampling 具有一些关联。

与 EM 类似，比较依赖于初始化设置，不同的初始化会得到截然不同的结果。由于非凸，只能取到局部最优值。

Stochastic VI

传统的 VI 不能处理大量数据。因此需要随机 VI 来处理。

思想：大数据采出子集，进行局部结构的优化，再更新全局结构。再进行下一次迭代。

原始的 ELBO 的 natural gradient 是这样的

$\nabla_{\lambda}^{\mathrm{nat}} \mathscr{L}(\lambda)=\left(\alpha+\sum_{i=1}^{n} \mathbb{E}_{\phi_{i}^{*}}\left[t\left(Z_{i}, x_{i}\right)\right]\right)-\lambda$

经过随机优化，得到 noisy natural gradient

$\begin{aligned} j & \sim \text { Uniform }(1, \ldots, n) \\ \hat{\nabla}_{\lambda}^{\text {nat }} \mathscr{L}(\lambda) &=\alpha+n \mathbb{E}_{\phi_{j}^{*}}\left[t\left(Z_{j}, x_{j}\right)\right]-\lambda \end{aligned}$

这样一个数据点就可以更新整个自然梯度。需要满足的前提是 noisy natural gradient 是无偏的，即$\mathbb{E}\left[\hat{\nabla}_{\nu} \mathscr{L}(\nu)\right]=\nabla_{\nu} \mathscr{L}(\nu)$。

Recipe

一般的分布遵循以下步骤即可近似出后验分布：

Start with a model
$p(\mathbf{z}, \mathbf{x})$
选择合适的变分分布
$q(\mathbf{z} ; \nu)$
根据两种拆分方式写出 ELBO，如
$\mathscr{L}(\nu)=\mathbb{E}_{q(\mathbf{z} ; \nu)}[\log p(\mathbf{x}, \mathbf{z})-\log q(\mathbf{z} ; \nu)]$
积分得到 ELBO
Example: $\mathscr{L}(\nu)=x \nu^{2}+\log \nu$
关于变分参数求梯度，优化 ELBO
Example: $\nabla_{\nu} \mathscr{L}(\nu)=2 x \nu+\frac{1}{\nu}$
$nu_{t+1}=\nu_{t}+\rho_{t} \nabla_{\nu} \mathscr{L}$

Black box VI

先积分 ELBO 再求梯度往往是比较困难的。是否可以先求梯度再积分，最后进行优化？

在推导模型时，求似然、后验、梯度等工作往往是费时费力的。能否将这些推理都放入黑盒中，我们最后只要输出后验？

Define

$g(\mathbf{z}, \nu)=\log p(\mathbf{x}, \mathbf{z})-\log q(\mathbf{z} ; \nu)$

可以推导出

$\nabla_{\nu} \mathscr{L}=\mathbb{E}_{q(\mathbf{z} ; \nu)}\left[\nabla_{\nu} \log q(\mathbf{z} ; \nu) g(\mathbf{z}, \nu)+\nabla_{\nu} g(z, \nu)\right]$

这样就把求梯度放在了积分里面。这样就可以从变分分布 q 中采样，用 Monte Carlo 估计出 q 的梯度，并进行随机优化，更新 q；迭代至收敛。

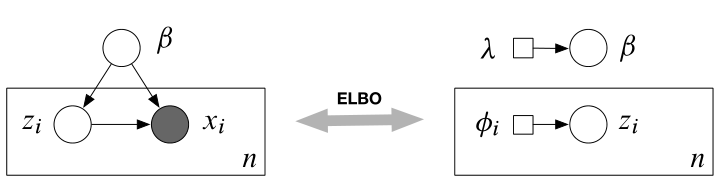
黑盒 VI 的主要目标是不论模型如何，我们只要做下面这三件事，其余的不用推理。最后黑盒可以输出近似的变分分布作为后验分布。

Black Box Criteria

sample from $q(\beta, \mathbf{z})$

evaluate $q(\beta, \mathbf{z})$ or function of $q$

evaluate $\log p(\beta, \mathbf{z}, \mathbf{x})$

有以下两种策略都符合 BBC：

Score gradients
Reparameterization gradients

Score Function Gradients

See score function, it is called likelihood ratio or REINFORCE gradient.

当$\mathbb{E}_{q}\left[\nabla_{\nu} g(\mathbf{z}, \nu)\right]=\mathbb{E}_{q}\left[\nabla_{\nu} \log q(\mathbf{z} ; \nu)\right]=0$，则 ELBO 的梯度可写为：

$\nabla_{\nu} \mathscr{L}=\mathbb{E}_{q(\mathbf{z} ; \nu)}[\underbrace{\nabla_{\nu} \log q(\mathbf{z} ; \nu)}_{\text {score function }}(\underbrace{\log p(\mathbf{x}, \mathbf{z})-\log q(\mathbf{z} ; \nu))}_{\text {instantaneous ELBO }}]$

它的 noisy unbiased gradient 可以用 MC 得到：

$\begin{array}{r}{\hat{\nabla}_{\nu} \mathscr{L}=\frac{1}{S} \sum_{s=1}^{S} \nabla_{\nu} \log q\left(\mathbf{z}_{s} ; \nu\right)\left(\log p\left(\mathbf{x}, \mathbf{z}_{s}\right)-\log q\left(\mathbf{z}_{s} ; \nu\right)\right)} \\ {\text { where } \mathbf{z}_{s} \sim q(\mathbf{z} ; \nu)}\end{array}$

更新 $q$ 时，有

$\nu=\nu+\rho\hat{\nabla}_{\nu} \mathscr{L}$

因此实际上需要做的步骤：

Sampling from $q(\mathbf{z})$
Evaluating $\nabla_{\nu} \log q(\mathbf{z} ; \nu)$
Evaluating $\log p(\mathbf{x}, \mathbf{z})$ and $\log q(\mathbf{z})$

这个方法适用于离散或连续的模型，但是 noisy gradient 的方差可能会很大。

Reparameterization gradients (Pathwise Gradients of the ELBO)

假设 $\log p(\mathbf{x}, \mathbf{z})$ 和 $\log q(\mathbf{z})$ 关于 z 可微，可以将 z 分解成如下形式：

$\begin{aligned} \epsilon & \sim \operatorname{Normal}(0,1) \\ z &=\epsilon \sigma+\mu \\ & \rightarrow z \sim \operatorname{Normal}\left(\mu, \sigma^{2}\right) \end{aligned}$

这样不确定性就被转移到了 $\epsilon$.

$\nabla_{\nu} \mathscr{L}=\mathbb{E}_{s(\epsilon_)}[\underbrace{\nabla_{z}[\log p(\mathbf{x}, \mathbf{z})-\log q(\mathbf{z} ; \nu)]}_{\text {gradient of instanneous ELBO }} \underbrace{\nabla_{\nu} t(\epsilon, \nu)}_{\text {gradient of transformation }}]$

它的 noisy gradient 可以写成：

$\begin{array}{r} \tilde{g}_{t}=\frac{1}{S} \sum_{s=1}^{S} \nabla_{z}\left[\log p\left(\mathbf{x}, t\left(\epsilon_{s}, \nu_{n}\right)\right)-\log q\left(t\left(\epsilon_{s}, \nu_{n}\right) ; \nu_{n}\right)\right] \nabla_{\nu} t\left(\epsilon_{s}, \nu_{n}\right) \\ {\text { where } \epsilon_{s} \sim s(\epsilon) \quad s=1 \ldots S} \end{array}$

这个方法要求模型必须可微。但是 noisy gradient 的方差是可控的。