任务场景

给定数据，真实的分布是未知的。我们学习的任务就是去拟合出真实的分布。现在我们给出一个真实分布是 GMM，在上面采样得到一组数据。你是否能够根据数据去拟合出这个分布？

1
2
GMM(means, variances, weights)
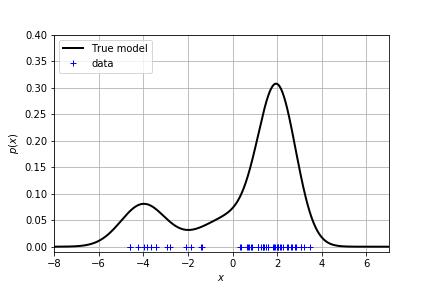
true_model = models.GMM([-4, 0, 2], [1, 2, .7], [0.2, 0.2, 0.6])

单峰分布

用高斯分布拟合

我们知道高斯分布是长这样的

  • $\mu$ is the mean of the Gaussian density
  • $\sigma^2$ is the variance of the Gaussian density
  • $\lambda = \frac{1}{\sigma^2}$ is the precision of the Gaussian density

（等等我们可以用 $\lambda$ 代替方差来写高斯分布）

为了估计真实的分布，可以采用最大化似然的办法得到均值和方差

1
2
3
N = len(X)
mean = np.sum(X)/N
var = np.sum(X**2)/N

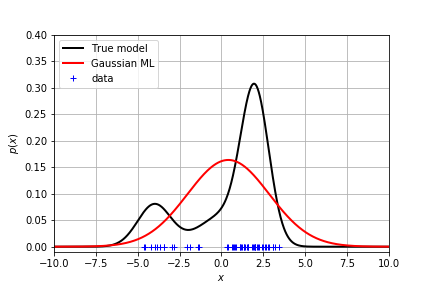
显然这个结果不能很好地拟合真实分布。

贝叶斯推理：加入均值和方差的先验

A common and convenient choice of prior for the Gaussian is the Normal-Gamma prior:

where:

$m_0$, $\kappa_0$, $a_0$ and $b_0$ are called hyper-parameters. They are the parameters of the prior distribution.

为了对 Normal-Gamma 分布有个形象的了解，可以绘图看到，它的均值和方差是服从这样的概率分布的

1
2
NormalGamma(mean, kappa, a, b)
ng_prior = models.NormalGamma(0, 2, 5, 6)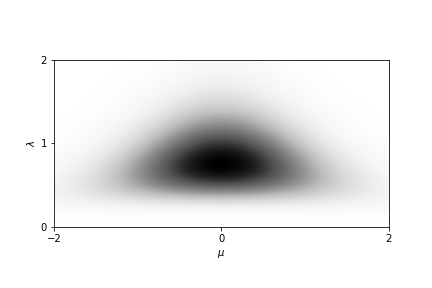

由于 Normal-Gamma 是 正态分布的 共轭先验，因此 Normal-Gamma 的后验有闭式解，且可以写成如下形式：

where:

$N$ is the total number of point in the the training data and $m_n$, $\kappa_n$, $a_n$ and $b_n$ are the parameters of the posterior. Note that they are different from the hyper-parameters !!

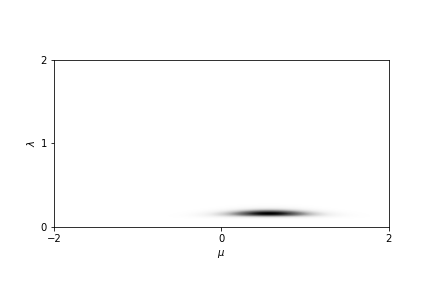
因此加入后验的影响后，均值和方差的分布成为更加聚集的一小团。

当需要做预测任务时，则需要把均值和方差边缘化（积分掉），得到数据分布。恰好这个分布是学生分布。由此可以得到每个数据点的概率密度：

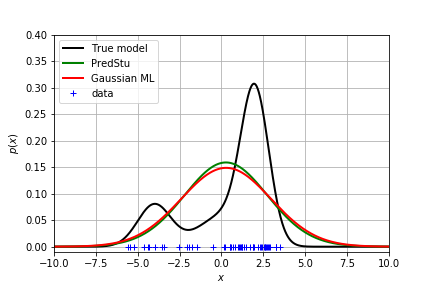
但是由于是单峰的，拟合效果还是很差！

多峰分布

用高斯混合模型拟合

我们尝试用 K 个不同的高斯分布来拟合真实分布：

  • $\boldsymbol{\mu}$ is the vector of $K$ means
  • $\boldsymbol{\lambda}$ is the vector of $K$ precisions
  • $\boldsymbol{\pi}$ is the vector of $K$ weights such that $\sum_{k=1}^K \pi_k = 1$

其中给不同高斯加的权重作为隐变量。

用 EM 算法求解参数

  • initialize the parameters of the GMM
  • iterate until convergence ($ \log p(\mathbf{x} | \theta^{new}) - \log p(\mathbf{x} | \theta^{old}) \le 0.01$):
    • Expectation (E-step): compute the probability of the latent variable for each data point
    • Maximization (M-step): update the parameters from the statistics of the E-step.

具体推导可以看 Expectation Maximization algorithm 以及 GMM

1
2
3
4
5
6
7
8
9
10
11
last_llh = -1e8
while 1e-2 < np.absolute(llh - last_llh):
    # E-step
    Z = gmm.EStep(X)
    
    # M-step
    gmm.MStep(X, Z)
    
    last_llh = llh
    llh = gmm.logLikelihood(X)
    print('log-likelihood:', llh)

具体的 EStep 和 MStep 可以看这里

不同的参数初始化得到的效果不同。这里给出了一个拟合得较好的分布：

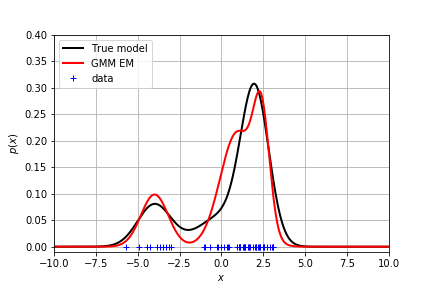
贝叶斯推理：加入先验

加入参数的先验：

如果仍旧想用 EM 算法求解参数，则在 M 步会直接把均值和方差算出来，而不是算出均值和方差的后验。因此不能用 EM 算法。

考虑到参数之间有相互依赖的关系，可以用 Gibbs Sampling 得到参数的后验分布。给出以下三个条件分布，在每次迭代中，都假设知道了条件值，采出样本。最终它们将趋向于真实分布。

latent variable $z_i$

mean and variance

We define the set of all data point $x_i$ that are assigned to the component $k$ of the mixture as follows:

and similarly for the latent variables $\mathbf{z}$:

where:

NOTE: these equations are very similar to the Bayesian Gaussian estimate. However, it remains some difference

weights

where:

1
2
3
4
5
6
7
8
9
10
for i in range(20):
    # Sample the latent variables
    Z = bgmm.sampleLatentVariables(X)
    
    # Update the parameters
    bgmm.sampleMeansVariances(X, Z)
    bgmm.sampleWeights(Z)
    
    # Just for plotting, this is not part of the Gibbs Sampling algorithm.
    plotting.plotGMM(bgmm.gmm, fig=fig, ax=ax, color='b', lw=.5, label='sampled GMM')

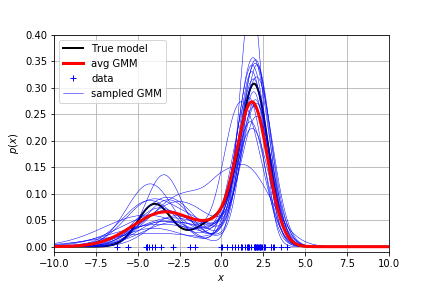
每次迭代的参数都可以生成一条蓝线。把蓝线加权平均得到了红线。看起来还是比较接近真实分布的。

相关教程